今回は、複雑なリズムを作るときに使われるテクニック、“メトリックモジュレーション”を解説します。
では、いってみよう!(๑˃̵ᴗ˂̵)و
“メトリックモジュレーション”とは?
まず、いきなりですが…
“同じ音価(音の長さ)を持つ音符”は、いくつも存在するのをご存知でしょうか。
たとえば
- 「BPM=120の4分音符」
- 「BPM=90の付点8分音符」
- 「BPM=60の8分音符」
はどれも500ミリ秒で同じ音価を持つ音符です。
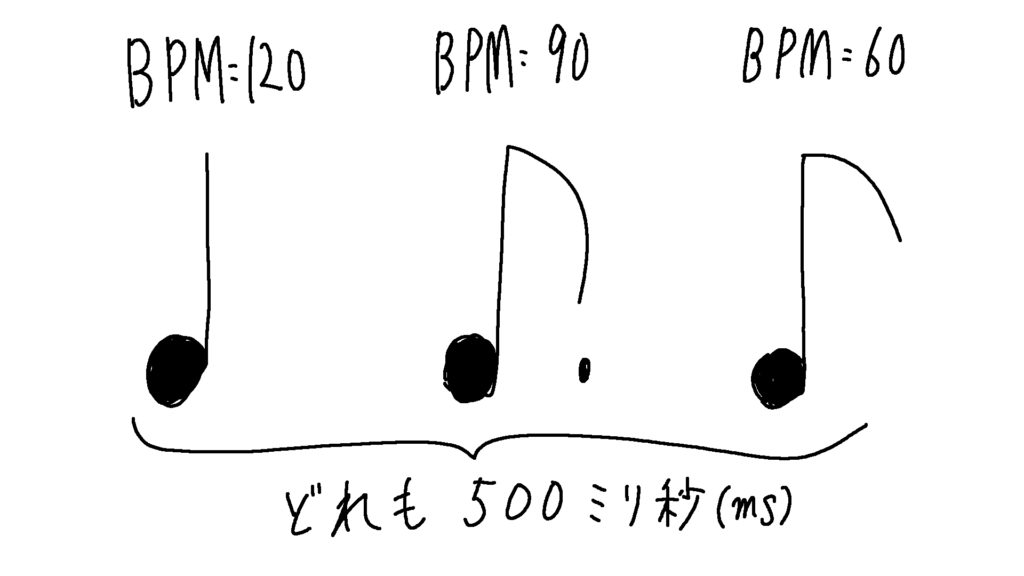
つまり、違うBPMで、同じ音価を持つ音符は複数存在します。
そして、このリズムの性質を利用して、
BPMが変わったように錯覚させる、もしくは前後のBPMに関連性を持たせた上でテンポチェンジをする手法を“メトリックモジュレーション” と言います。(※)
その名の通り「リズムの転調」とも言えるでしょう。
※「BPMが変わったように錯覚する」と、「前後のBPMに関連性を持たせたテンポチェンジ」は、表裏一体の関係です。
最終的に2つの現象を区別するのは「使い手・聴き手の解釈」です。
たとえば、この曲↓はAメロに対してBメロのリズムのノリが倍の長さになっています 。
星野源 – 恋
いわゆる、”ハーフタイム“のリズムですよね。
“ハーフタイム(半テン)”や、“ダブルタイム(倍テン)”と呼ばれるリズムは、”メトリックモジュレーション“の一番単純なカタチだと解釈できます。
…ただ、通常は「メトリックモジュレーション」と言う場合、もう少し複雑な関係性にある”同じ音価を持つ音符”への解釈の変更を指します。
たとえば、この動画のリズムパターン。
途中でハイハットで刻んでいるビートが、8分音符から3連符に変化しています。
そして、スネアドラム(アクセント)の位置の変化でテンポ自体が変わったように聴こえますね。
典型的な”メトリックモジュレーション“を使ったリズムトリックです。
“メトリックモジュレーション”を使用したリズムトリック
先ほどのリズムは、あくまで一例です。
“メトリックモジュレーション“を使ったリズムのアイデアは、無数に考えられます。
したがって、最終的には「数値計算」と「アイデア次第」になります。
ただ、基本的な仕組みはドラム単体の音源で聴くと分かりやすいので例を用意しました。
以下の2つのリズムはどちらも同じBPM=128で演奏されています。
譜例① 「付点8分音符」を1拍と捉えたリズムパターン

譜例② 「4分音符」を1拍に捉えたリズムパターン

同じBPMにもかかわらず、この2つのリズムから感じるリズムのノリや速さは明らかに違うはずです。
それは「アクセント(スネアドラム)の位置」や「ビートの刻み方」が違うためです。
具体的には、
譜例①は、「”付点8分音符”を1拍と捉えたリズムパターン」
譜例②は、「”4分音符”を1拍に捉えたリズムパターン」
になっています。
メトロノームありで交互に演奏すると、こうなります。
いかがでしょうか。
特に譜例①のリズムは「”メトリックモジュレーション”使ってます感」がありますね。
作曲への応用 Tips
ここで、ちょっとした作曲への応用例を紹介。
下記の二つのリズムは、バスドラムの打点が一緒です。

このようなリズムパターンは、 リフやフレーズをバスドラムのリズムに合わせると
リフの聴こえ方が途中で変わる面白い効果を演出できます。
使用例
実際の曲中での”メトリックモジュレーション“の使用例を紹介します。
Dream Theater – Moment Of Betrayal
2回目のAメロ部分(2:00~)でドラムによる”メトリックモジュレーション“を使ったリズムトリックが使用されています。

僕の耳が正しければこんな感じ。
まるで細かくテンポが速くなったり遅くなったりしているようですよね。
KHUFRUDAMO NOTES – YAMATO
“メトリックモジュレーション“を利用した整合性を持ったテンポチェンジの例です。
拙作、KHUFRUDAMO NOTESの「YAMATO」は
中間部分(1:44~)でBPM=150からBPM=112.5にテンポチェンジをしています。
これは、最初のBPM(=150)の「1拍3連」の音価が、テンポチェンジ後のBPM(=112.5)の「16分音符」の音価と等しくなる関係になっています。
KHUFRUDAMO NOTES – KEGON
KHUFRUDAMO NOTESの「KEGON」は、中間部分でBPM136からBPM=204にテンポチェンジして、またBPM=136に戻ります。
これはBPM=136の1拍6連符と、BPM=204の16分音符が等しくなる関係になります。
↓動画の37分あたりから、テンポが戻る部分の“メトリックモジュレーション“と“変拍子”を絡めたテンポチェンジの解説をしています。
坂東慧(T-SQUARE) – Paradigm
2:59あたりから、3連を使った分かりやすい”メトリックモジュレーション“です。
その他にもドラムソロ中に、多数”メトリックモジュレーション“を使ったフレーズが散りばめられています。
Gergo Borlai – Metric Modulation Madness
曲名から「”メトリックモジュレーション”を使いまくる決意」が溢れ出ているこの曲。笑
“メトリックモジュレーション“を使用した浮遊感を覚えるリズムをたくさん聴けます。
同じテンポ(BPM)での色々なリズム解釈がよく分かる曲です。
Q.テンポチェンジに使うには?
メトリックモジュレーションをテンポチェンジに使うためには「任意の音符同士が、同じ音価になるBPM」を計算する必要があります。
メトリックモジュレーションの計算方法
まず、テンポチェンジ前の音符とテンポチェンジ後に等しい音価にしたい音符を”分音符”で無理やり表したもの(※)をy分音符とします。
よく使いそうなy分音符の値は
- 8/3分音符(付点4分音符)
- 16/3分音符(付点8分音符)
- 8分音符
- 16分音符
- 12分音符(1拍3連)
- 20分音符(1拍5連)
などがあると思います。
※他のy分音符の値を求める方法は、こちらの記事を参考にしてください。
これを踏まえた上で…
y分音符の音価と、テンポチェンジ前の音符の音価が等しくなるBPMを求める計算式は
60000(ms)÷ ( テンポチェンジ前の音符の音価(ms) × y ÷ 4 )
=y分音符がテンポチェンジ前の音符と等しくなるBPM
となります。
…と言われても、まだピンときませんよね?笑
たとえば、テンポチェンジ前のテンポがBPM=120だとします。
このBPM=120の4分音符の音価(500(ms))と、同じ音価を持つ付点4分音符(8/3分音符)が存在するBPMを求めたい場合
60000(ms) ÷ (500(ms) × 8/3 ÷4)
= 60000(ms) ÷ 1000/3
= 180(BPM)
となり、「BPM=120の4分音符と等しい音価を持つ付点4分音符が存在するのは、BPM=180だ」と分かります。
メトリックモジュレーションの計算フォーム
…とは言え、毎回こんな面倒な計算やりたくないですよね?
そこで!
「BPM」や「テンポチェンジ前の音符の種類」を指定するだけで、メトリックモジュレーションに関係する情報が簡単に調べられるウェブアプリ↓を作りました!
ご自由にお使いください!(๑˃̵ᴗ˂̵)و
リズムについてさらに詳しく書いた記事もあります。興味のある方は是非こちらもどうぞ!