この記事は、僕が10年以上考えてきた「ジャンルや解釈に左右されない「リズム」の仕組み」のまとめです。
仰々しいタイトルですが、最終的に「納得できる理解の仕方」は人によると思います。
使えそうな所は使うなど、各自で有効活用してほしいです!
では、いってみよう!(๑˃̵ᴗ˂̵)و
はじめに: リズムを構成要素のレイヤーで考える
“リズム”という言葉には、色々な意味や解釈が存在します。
したがって、解釈のズレは避けたいです。
そこで、まず“リズム”に関係する要素を”抽象度で分類”して図↓にしました。
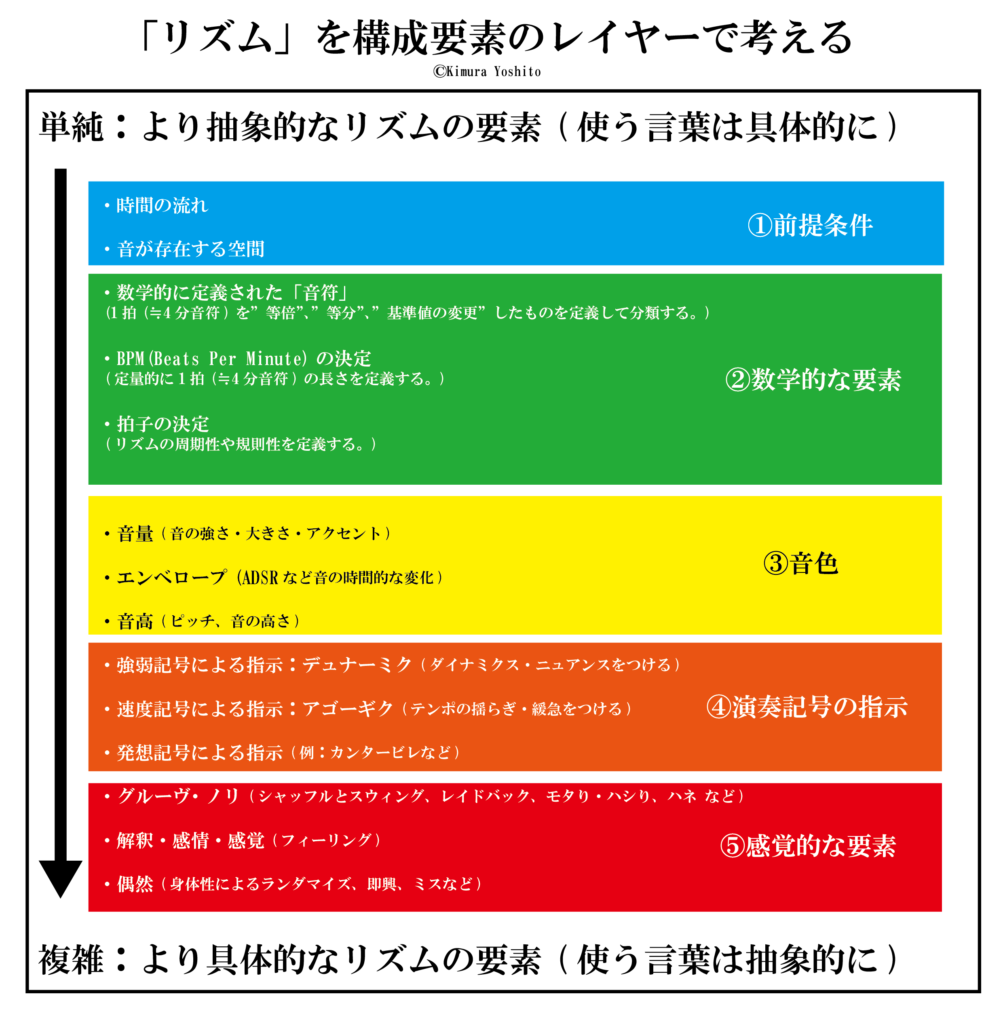
はじめに、この図に書かれている内容を説明をします。
それぞれのレイヤーの説明
レイヤー①前提条件

音楽は絵や彫刻と違い「時間芸術」です。
時間の流れがあり、音波が伝わる環境でなければ音楽はできません。
(つまり当たり前すぎる内容です。)
レイヤー②数学的な要素

「音符」や「拍子」や「BPM」など、数学的に定義できる部分です。
実際に演奏する”リズム“に対して、かなり抽象度の高い要素になります。
しかし、定量的にリズムを考えるのには適しています。
レイヤー③音色

音楽では、さまざまな種類の音が使われます。
“音の三要素“は
- 「音の大きさ」
- 「音の高さ」
- 「音色」
と言われます。
これらに加えて「エンベロープ」も、「音色」に関わる重要な要素です。
したがって、「エンベロープ」を「音色」と同じレイヤーにまとめました。
ちなみに、「エンベロープ(音の時間的な変化)」 を表すパラメーター「ADSR」とは
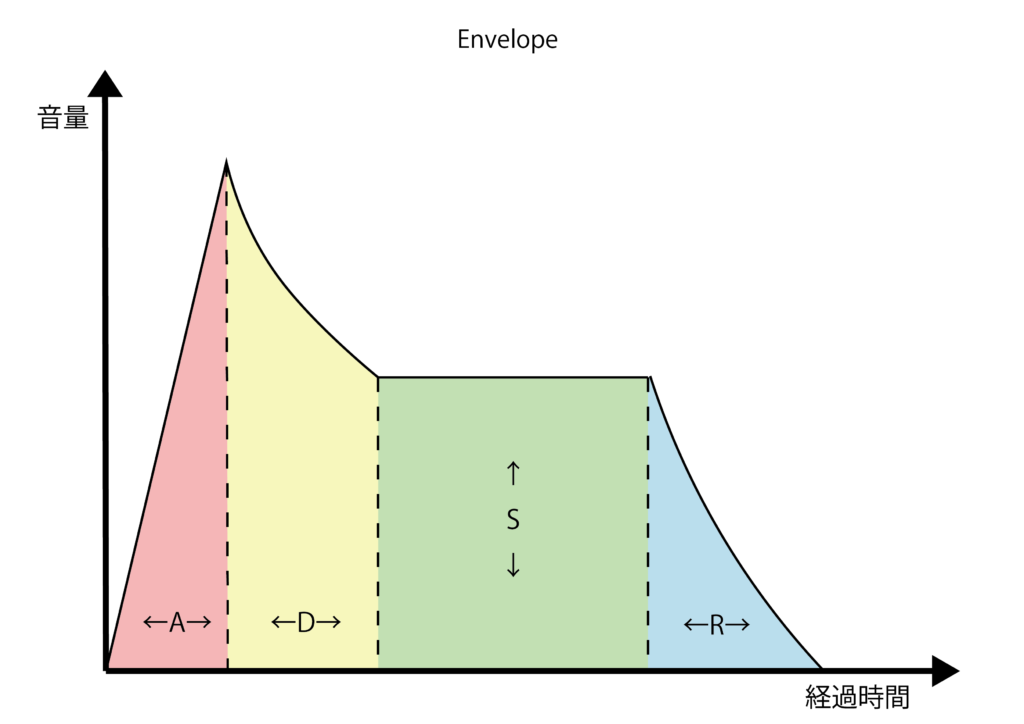
- A.アタック・タイム:音を出してから最大音量に到達するまでの時間
- D.ディケイ・タイム : 最大音量からサスティーンレベルの音量に減衰するまでの時間
- S.サスティーン・レベル : 減衰後の音量の保持量
- R.リリース・タイム : 音を出すのをやめてから音が消えるまでの余韻の時間
の頭文字をとった略称です。
レイヤー④演奏記号による指示

たとえば
- フォルテ(強く)
- ピアノ(弱く)
- リタルダンド(徐々に遅く)
- アッチェレランド(徐々に速く)
など演奏記号による指示も、”リズム“に関係する大切な要素です。
ただ、演奏記号の指示に大まかな方向性はあるものの具体的な数値ではありません。
それなりに演奏者が裁量を持てる要素なので、言葉の抽象度は高めです。
レイヤー⑤感覚的な要素

“グルーヴ”、”ノリ”など「実際に演奏するリズム」に対して一番具体的な要素です。
しかし、ジャンル・演奏者の習熟度・解釈・文化・文脈などによって捉え方が異なるため、定量的な議論が難しく、かなり抽象的な言葉です。
“②数学的な要素”に着目するメリット
この記事では、以上5つのレイヤーのうち“②数学的な要素“に着目します。

なぜなら、図の下のレイヤーへ行くほど

“リズム”に対してのアプローチは具体的なる反面、使用する言葉は抽象的になるからです。
たとえば、“⑤感覚的な要素“に分類した“グルーヴ“は、「数値で量れないカッコいいリズムのノリや演奏」を指す言葉です。
ミュージシャン同士でなんとなく概念を共有しているものの、はっきりとした定義があるとは言い難い言葉です。
したがって、 “リズム“を定量的に論じる場合は慎重な扱いをするべきだと考えます。
BOØWY、ザ・ブルーハーツ、GLAYなど、数々のアーティストのプロデュースを手掛けた佐久間 正英さんも
「グルーヴ」は逃げ道として非常に便利な言葉。
よって、安易にこの言葉を使わないように。『直伝指導! 実力派プレイヤーへの指標 How to be a professional player? プロになること、目指すこと』 p.29
と自身の著書の中で書いています。
反対に、図の上に行けば行くほど“具体的なリズムのアプローチから離れていく代わりに、言葉としては論理的・数学的に定義できる部分が多くなります。
特に“②数学的な要素”の内容は
- “リズム”を体系的に捉えられる。
- 言葉や概念の定義が比較的はっきりしている。
- ジャンル・演奏者の習熟度・解釈・文化・文脈などによる理解の差が生じにくい。
ものであり、“リズム”概念の基礎だとも言えます。
もちろん、最終的には全てのレイヤーの要素が統合されて演奏されるので、特定の要素だけで良い演奏をするのは難しいです。
ただ、 まずは「基礎である“②数学的な要素”への理解は重要だ」と考えます。
それでは、これらの内容を踏まえた上で「リズムの把握の仕方」を見ていきましょう。
★12種類のリズムでどんなリズムも把握できる
古今東西の音楽には、さまざまな”リズム”が使われています。
しかし、僕は最低12種類のリズムを知るだけで、実質的に“全てのリズム”の把握に応用できると考えています。
リズムを束で考える(12個のリズムを考える)
まず、単純化のために
ある打点で音が「出ている・出ていない」
の2通りだけを考えます。
●←音を出す 〇←音を出さない
(※音色や音高は無視して、音量を「0」か「1」で捉えるわけです。)
次に、「グループ化された打点」を「束」と表現します。
たとえば
● 〇 | ● ● | 〇 ● | 〇 ●
↑2つずつ区切ったリズムは「2の束のリズム」が繋がっている とし、
● 〇 〇 | ● 〇 ● | ● 〇 ● | ● 〇 ●
↑3つずつ区切ったリズムは「3の束のリズム」が繋がっている とします。
「2の束のリズム」と「3の束のリズム」
そして、これらのリズムの組み合わせを考えます。
※以下では●を四分音符、〇を四分休符で表現します。
2の束のリズム
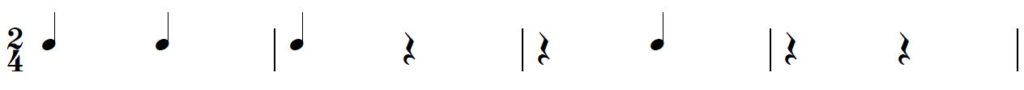
2の束のリズムは、以上の4通りです。
3の束のリズム

3の束のリズムは、以上の8通りです。
よって「2の束のリズム」と「3の束のリズム」 の計12通りの組み合わせが存在します。
これが 「12種類のリズム」です。
そして、この「12種類のリズム」に対して
- ①組み合わせる
- ②等倍・等分
- ③基準値の変更を行う
操作をすれば、人間に知覚できる全てのリズムを考えられます。
①組み合わせる
まず、「①組み合わせ」による変形を考えます。
たとえば、「4の束のリズム」の組み合わせは「2の束リズム」2つ分で理解・表現できます。
例を挙げると、この「4の束のリズム」 ↓は
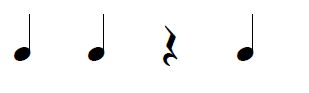
「2の束リズム」の4通りの組み合わせのうち
↓このリズムと

↓このリズム

を順に繋ぎ合わせたと理解できます。
他には、こんなリズム↓なら

「2の束リズム」の↓このリズムと

「3の束リズム」の↓このリズム

を順に繋ぎ合わせたと理解できます。
したがって、計12通りの「2の束のリズム」と「3の束のリズム」 の組み合わせだけで、色々なリズムを理解できます。
4の束のリズム
ちなみに、「4の束」の16通りの組み合わせ↓も覚えておくと色々なリズムに素早く対応できるので便利です。
なぜなら、実際の世の中には4拍子の曲が圧倒的に多い上に、16分音符を考えるときに役に立つからです。

②等分・等倍する
次は、組み合わせたリズムの等分・等倍にあたるリズムを考えてさらに色々なリズムへ適応を図ります。
たとえば、このリズム↓に対して

このリズム↓ は、

BPM(テンポ)が同じ場合、ちょうど速さが倍のリズムになります。
逆も然りです。
つまり、どちらも打点のタイミングの”比”が同じ種類のリズムと解釈できます。
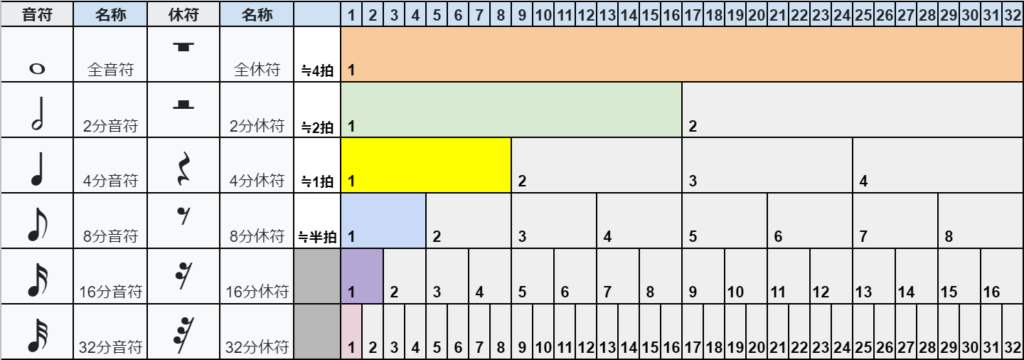
たとえば、4の束のリズム 16通りを理解すると

その倍のリズム↓、

さらにその倍のリズム↓

なども、それぞれ同じタイミングの比で打点が構成されているので理解できます。
③基準値を変更する
最後に”基準値を変更する”と、連符にも対応できます。
たとえば、「3の束リズム」の組み合わせと

この2拍3連符のリズムの組み合わせは
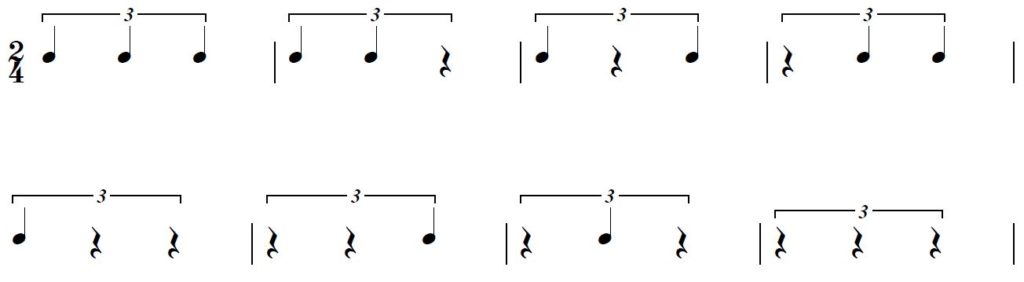
それぞれ同じタイミングの比で打点が構成されています。
関連性を持たせて理解すると、全て暗記しなくてもそれぞれの関係性からリズムを理解できるのです。
連符の比の意味①
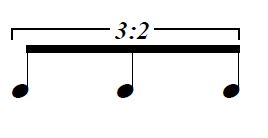
ちなみに、よく見る連符の
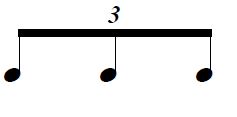
↑この書き方は省略形で、
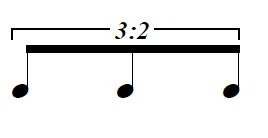
このように比の形で書くのが丁寧な書き方です。
「3 : 2」の場合、
「8分音符(音符の形や符尾・連桁の数から判別する)が2個分の長さを3等分している」
という意味になります。
さらに①②③を組み合わせて、変拍子や連符を考える
最後に変拍子や連符への対応を考えます。
これも、 「2の束のリズム」と「3の束のリズム」 の12種類の組み合わせから考えます。

↑5拍子なら「2+3」または「3+2」
6拍子は「2+2+2」または「3+3」
7拍子は「2+2+3」や「3+2+2」…
みたいに、どんな変拍子の理解にも応用できます。
さらに、連符はこのように考えた拍子(リズムのまとまり)↓の

基準値を変更して連符として捉えればいい↓ので、

これで連符にも対応できます。
ただ練習は必要
たった12種類のリズムから色々なリズムを考えてきました。
この視点を持っていると、一見難しそうなリズムでも細かく見ていけば単純なリズムの組み合わせだと分かります。
ただ、一方で「理解できる」と「演奏できる」は違います。
実際の演奏や作曲でスムーズに使うには、ある程度のトレーニングが必要だと思います。
応用と併用
ちなみに、「リズムを簡単に把握する」視点では、言葉に当てはめて考える方法も有効です。
たとえば、5連符は5文字の言葉(「メロンパン」や「夏休み」など)に当てはめます。

細かい連符を演奏する時に便利な方法です。
※実際の演奏では、適宜理解しやすい方法を使うと良いと思います。
リズムの実時間の長さ(音価)を考える
BPMを決定する(4分音符の音価を定義する)
ここまでの内容で、さまざまなリズムに対応できると思います。
しかし、実はまだ理屈としては十分ではありません。

上で紹介してきたリズム(=音符の種類)が示すのは、相対的な音符の長さの違いです。
リズムをしっかりと定義するには、「音符の時間的な長さ(音価)」を紐づける必要があります。
なぜなら、“同じ音価(音の長さ)を持つ音符”は、いくつも存在するからです。
たとえば
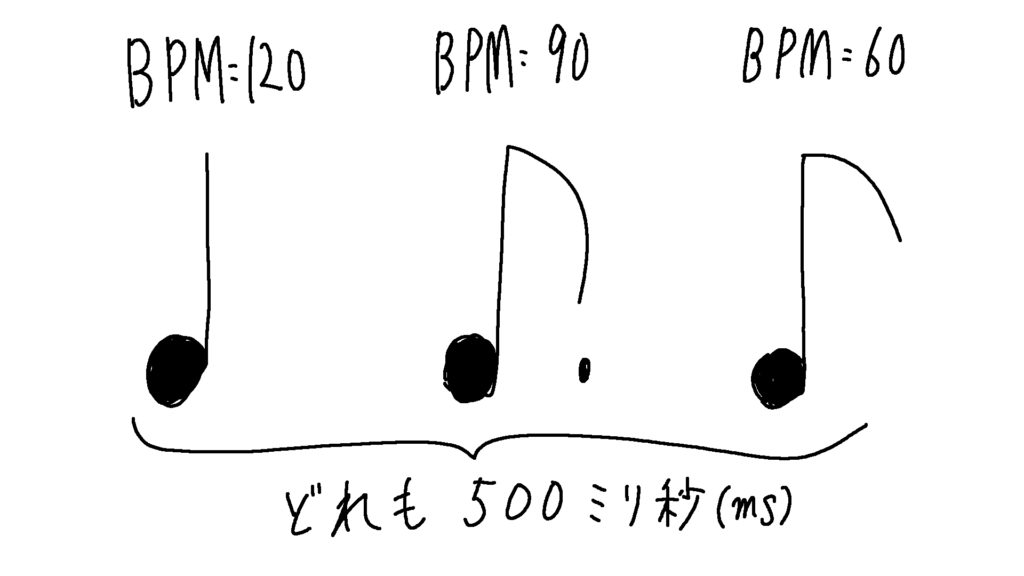
「BPM=120の4分音符」と「BPM=90の付点8分音符」と「BPM=60の8分音符」は、どれも500ミリ秒で同じ音価を持つ音符です。
(これは後述の「メトリックモジュレーション」の仕組みにも繋がる話です。)
したがって、
BPMを指定して4分音符の「時間的な長さ」を定義する必要があります。
(…まわりくどい書き方ですが、当たり前のこと言ってるだけです。)
音価を計算する式①
では、BPMを決める必要性が分かったところで、実際に音価を計算してみましょう。
音価を考える時に使う数値は、以下の5つです。
- 60000ms (6万ミリ秒=60秒 つまり、1分)
- BPMの値(この値で60秒を分割して、分割した1つ分の長さを4分音符の長さとする)
- 分音符の種類(…全音符(4分音符×4)を何分割するか)
- 付点の数(分音符にいくつ付点が付くか)
- 連符の分割数(それを何連符に分割するか)
まず、4分音符の音価を求めるために
・4分音符の音価(ms) = 60000ms÷BPMの値
の計算をします。
たとえば、BPM=60の場合
60000÷60 の計算をすればいいので、BPM=60での4分音符の音価は1000ms(=1秒)になりますね。
そして、そこから全音符の音価を求めます。
4分音符が4つ分で全音符の長さ になるので
・全音符の音価(ms) = 4分音符の音価(ms) × 4
となります。
全音符の長さを先に求める理由は、基本的には”音符の種類“を求めるには全音符を”2つの概念“で分割すればよいからです。
具体的には
①「分音符」(「4分音符」や「2分音符」など)
②「連符」
の2つです。
だから、全音符の長さを求めたら、あとは任意の概念で分割すればOKです。
現在の記譜法を考える
これまでの歴史を振り返って、音楽の発展・複雑化をもたらした大きな要素は
- 「記譜法の確立」
- 「録音技術の発明」
- 「コンピューター」
だと言われています。
ここからは、そんな「記譜法」に関連した内容を考えます。
「1拍」を考える

音楽をやっていると何気なく「1拍」という言葉を使います。
しかし、実は「1拍」は曖昧な言葉です。
たしかに、「1拍」 は基本的に4分音符を指す場合がほとんどです。
一方で、付点4分音符や、8分音符や、2分音符が「1拍」を指す場合もあります。
…つまり、最終的には譜面がなければ 「1拍」 は個人の主観に委ねられるわけです。
したがって、あえて「1拍」を説明するなら
「リズムをとるとき(ダンスのカウントなど)に「感覚的に単位として考えるリズムの長さ」であり、多くの曲の場合それが4分音符である。」
あたりが妥当な落としどころかな…と思います。
なぜ3連符は安定して存在できるのか

子どもの頃、「1÷3=0.333333…で割り切れないよな…3連符って不安定なのかな?」と思っていた時期がありました。
結論を先に言うと、「答えが10進法で割り切れない数(循環小数)になるのと、等分できるかは関係ない」が答えです。
理解している人には、当たり前かもしれません。
しかし、かつての経験から「ここを理解しないと混乱しそう」と思ったので、具体的に説明します。
先ほど、60000ms(=1分=60秒)をBPMの値で分割して4分音符(≒1拍)の音価を“定義”しました。
つまり、3連符は「”1と定義したもの”を3で割っている」のです。
たとえば、BPM=100の4分音符の音価は 60000ms÷100(BPM)=600msです。
実際に、これを3で割って”1拍3連符”にすると、普通に割り切れます。(600ms÷3=200ms)
「いや、でも…BPM=60とかの場合、4分音符の音価は1000msになるから、3で割り切れないのでは…?」
と思うかもしれません。
確かに、この場合3で割り切れません。
しかし、こちらも「1分という時間を60秒としている」から割り切れないだけです。
「割り切れない」=「等分ができない」ではありません。

ちなみに、時間に60進法(1分が60秒など)を使う理由は…
「60」という数字は
- 高度合成数(60までの数で、最も約数の多い数字(約数が12個ある))
- 100までの数の中で見ても、最も約数の多い数字のひとつ(他は72、84、90、96)
- 1~6までの数字で割り切れる
ので、計算するときに便利だかららしいです。
https://ja.wikipedia.org/wiki/%E9%AB%98%E5%BA%A6%E5%90%88%E6%88%90%E6%95%B0
「拍子」を考える
3/4拍子と6/8拍子の違い
「3/4拍子と6/8拍子は分数で考えると同じ量なのに、何が違うの?」と思いませんか?
約分をすると、どちらも3/4になりますしね。
これに対しては、「拍子の分数は、3/4拍子は「単純拍子」、6/8拍子は「複合拍子」と分類されていて3/4拍子は3拍子、 6/8拍子は2拍子でとるんだよ~」
みたいに説明されますし、実際(特にクラシックでは)その通りです。
しかし、もう少し踏み込んで考えると、6/8拍子は「3と2のポリリズム」を表したい拍子であると考察できます。
6/8拍子の「1拍」は、4分音符ではなく、付点4分音符です。
つまり、6/8拍子は「3の束のリズム」と「2の束のリズム」が同時進行するリズムだと解釈できます。
したがって、 3/4拍子と6/8拍子をわざわざ分けたのは、同じ長さの区間のリズムでも、「ポリリズムと非ポリリズムを区別したい」欲求があったからと僕は理解しています。
( ポリリズムは別記事で詳しくまとめました。)
数学的には同じことでも違うリズム
他にも「4拍子の3連符表記」、「12/8拍子」、「シャッフル」、「スウィング」など数学的には同じリズムでも、それぞれ微妙に違うリズムを指す場合があります。
これは、抽象度が低い要素(⑤感覚的な要素など)での解釈の多様性

が関係していると考えています。
僕の「拍子」に対しての考え
主にクラシック音楽においては、拍子ごとにアクセントの決まり※があります。
※「2拍子は1拍目を強く、2拍目を弱く…」など
しかし、クラシックと違う考え方をした方が、合理的な場合もあります。
僕は、リズムを数学的に捉える場合「拍子」は「1拍」とは違う、「もう一つ上の階層でリズムをグループ化したもの」と考えると良いと思います。
もちろん、従来のルールをある程度守らなければ他人に伝わらないので、守れる部分は守るべきだと思います。
しかし、現代は昔に比べてはるかに多様な音楽があります。
演奏する際にリズムが分かりやすく、表記が簡潔になる「拍子」を選ぶのも大切な視点だと考えます。
「分音符だけの世界」を考える
通常「〇分音符」の〇に当てはまる数字の種類は、「2の冪( 2の累乗数)※」ですよね。
※1(全音符)、2、4、8、16、32…
ここで
「なぜ3分音符や、5分音符は無いのか?」
と疑問を持つ人もいるでしょう。
僕も「なんでかな~」と思っていた時期がありました。
色々と考えた結果、今のところの結論は「今の表記の方が便利だから」です。
実際に比較してみましょう。
“分音符“が“分”けているのは、”全音符“↓ですよね。

つまり、3分音符が存在するとすれば「全音符を3等分した長さの音符」になるはずです。
現在この「全音符を3等分した長さの音符」を表しているのは…
↓4拍3連符です。

他も確認してみましょう。
・6分音符 = 2拍3連

・12分音符 = 1拍3連

・24分音符 = 半拍3連(=1拍6連)

いかがでしょうか。
僕は現在の表記の方が便利だと思います。
なぜなら、現在の表記は「3の束のリズム」=「3連の感覚」を体得すれば、他のリズムも、その応用で比較的スムーズに理解・演奏可能になるからです。
一方で、「分音符だけの表記」にすると直観的に感覚を掴むのが難しくなる上に「1拍」をとるポイントが分かりずらくなり不便です。
(ただ、音ゲー界隈では「12分音符」や「24分音符」という用語があるので、今の表記に慣れてすぎている部分もあるかもしれませんが)
そして、そもそも仮に「分音符だけの表記」にした場合、楽譜に書き込む音符の表記が煩雑になる可能性が非常に高いです。
だから、“「分音符」の種類に使う数は「2の冪」だけにして、他の数で分割を行う時は「連符」を使う”現在の「全音符を2段階の概念で分割するシステム」が採用されたのだと思います。
なぜ現代の記譜法では「分音符」と「連符」を併用しているか分かる気がします。
このあたりの内容は、動画でも解説してみました。
「付点」を考える
音符を表す仕組みの中に「付点音符」があります。
「分音符だけの世界」を考えたときと同様、「付点音符」表記が無くても「分音符」と「連符」だけでもリズムを表せます。
ではなぜ、この概念が必要なのでしょうか。
こちらも、今のところの結論は、「便利だから」です。笑
僕がそう考える理由は主に2つあります。
①3の束のリズムを一つの音符で簡潔に表せる
世の中には4拍子の曲の次に、3拍子…というか「3の束のリズム」を使った曲が多いです。
しかし、「付点音符」がなければ、「3の束のリズム」 に値する音符を1つで書けません。
たとえば、3拍を表すときに↓ いちいち音符をタイでつなぐよりも

↓ 付点2分音符をひとつ書く方が、楽で分かりやすい場合が多いです。

また6/8拍子は、「2拍子」と考えられ「1拍」=付点8分音符で表現されます。

こんな表現をするために、付点音符はとても便利です。
②2の冪の連符を分かりやすく書ける
付点音符のもう一つの利点は、2の冪の連符※を分かりやすく表現できる点です。
※2連符、4連符など
これは「付点音符」が、3の束を 2の冪の数で分割する2の冪の連符と実質同じだからです。
たとえば、4連符↓を書くよりも
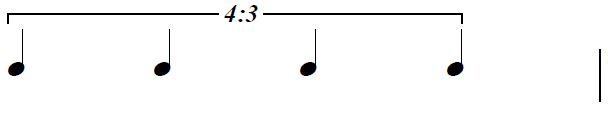
↓付点8分音符で表した方が、リズムを掴みやすいです。
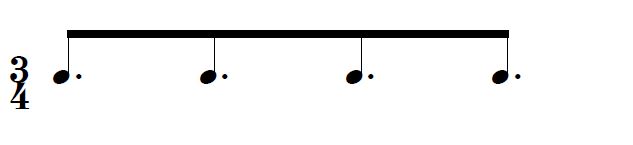
これは、
多くの人が4分音符=「1拍」を基準にリズムをとるため、「付点音符」でリズムを考えると、そのまま「1拍」の基準を変えずに対応できるためだと考えました。
一方、上の 4連符(2の冪の連符表記)の場合、 4分音符ではない分音符(この場合3の束のリズム) を「1拍」 と捉え直し、さらに、改めて2の冪の数の連符(この場合4)で分割する必要があります。
だから、「2連符」や「4連符」などの表記はリズムを掴みづらいのだと思います。
付点が2つ以上の付点音符
付点の数が2つ以上ある付点音符も存在します。
付点の数が2つなら「複付点音符」

3つなら「3重付点音符」

4つなら「4重付点音符」と呼びます。

…ぶっちゃけ曲に使われているのは、ほぼ見たことありませんが…笑
「付点」の数をd個とすると 付点音符の音価は
付点が付いた分音符の元の長さ(ms)×{2 – (1/2d)}
で表せます。
また、付点部分だけの音価は
付点が付いた分音符の元の長さ(ms) ×{(2d)-1} /2d
で求められます。
つまり…
「付点音符」は元の音符の1.5倍
(元の音符の長さの×0.5の長さが付点として付加される。)
「複付点音符 」 は元の音符の1.75倍
(元の音符の長さの×0.75の長さが2つの付点として付加される。)
「3重付点音符 」 は元の音符の1.875倍
(元の音符の長さの×0. 875の長さが3つの付点として付加される。)
の音価を持つ音符になるわけです。
付点が4個以上の付点音符も、同様の考え方で求めます。
(…ただ、「いつ使うねん」とは思います…笑)
現在の記譜法の「5」への適応力の低さ
ここまで現在の記譜法のメリットを紹介してきました。
反対に、現在の記譜法のデメリット…というか弱点だと思う部分を紹介します。
それは、1~8の数の中で
「5」のまとまりだけ「1つの音符で表す表記」が無い点です。
たとえば、「1拍」=4分音符とした場合…
- 「1拍」…4分音符
- 「2拍」…2分音符
- 「3拍」…付点2分音符
- 「4拍」…全音符
- 「6拍」…付点全音符
- 「7拍」…複付点全音符
- 「8拍」…倍全音符
このように、8拍までの「5拍」以外は「1つの音符で表す表記」があります。
簡単に表せないものは、無意識に使用する選択肢から除外されやすくなると考えられます。
たとえば、 昔の音楽の主流だったモノフォニー(単旋律)からメロディと和声(ハーモニー)が複雑化したのは、「現在の記譜法」が複雑な和音やメロディを書き易かったためと言われています。
反対に、現在よく耳にする曲の「リズム」の複雑性は、「メロディ」や「ハーモニー」に比べて随分低い気がするので、「こういった記譜法の弱点が影響しているのでは?」と思います。
リズムあれこれを計算で求める
では、音価を計算する式①に引き続き、リズムに関係する数値計算を考えていきます。
音価を計算する式②
今まで見てきた内容を全てを踏まえて
- 分音符の種類(…全音符をまず何分割するか)を n
- 付点の数(分音符にいくつ付点が付いているか)を d
- 連符の分割数(それを何連符に分割するか)を t
とすると
[(60000(ms)÷BPM×4)÷n}×2 – (1/2d)]÷t (ms)
という式になります。
「分音符だけの世界」を考えるメリット
「分音符だけで捉えた表記」 は演奏にあまり適さない捉え方と言いました。
しかし
- 「符尾・連桁の数を求めるとき」
- 「メトリックモジュレーション」を考える時の「同一の音価を持つ音符の種類」を割り出すとき(くわしくは後述)
- 「ポリリズム」を考えるとき
などでは、「分音符だけで捉えた表記」が役に立ちます。
「分音符だけの世界」で考えた場合の「分音符(x分音符)」のxの求め方
あらゆる音符を「分音符だけで捉えた表記」に変換するためには以下の計算をします。
全音符の音価(ms) ÷ 指定した音符の音価(ms) = x
この計算式で求めた値を使うと、音符を「分音符だけで捉えた表記(x分音符)」として表せます。
先ほど紹介した「4拍3連」も、音価を求めてこの式にぶち込むと、「3分音符」だと分かります。
連符の符尾・連桁のしくみ
基本的に連符の「符尾・連桁の数」は(本来の2の冪で表す)分音符を基準に決定できます。
たとえば、
- 8分音符の「符尾・連桁の数」は1つ
- 16分音符の「符尾・連桁の数」は2つ
ですよね。
このとき、ある連符の音価L(ms)が
8分音符の音価(ms) ≧ 連符の音価 L(ms) > 16分音符の音価(ms)
となる場合、この連符の「符尾・連桁の数」は1つになります。
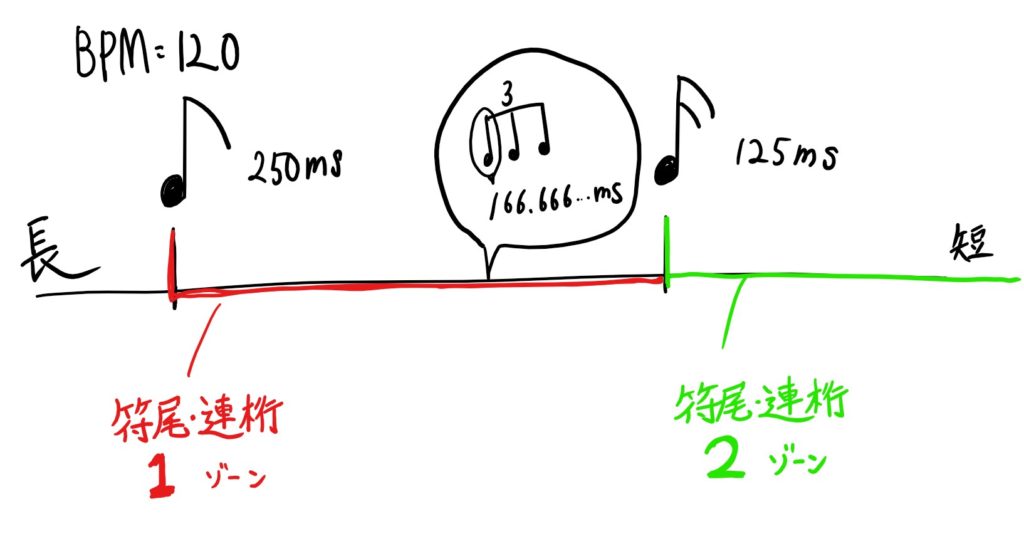
たとえば、連符をBPM=120の「1拍3連」で考えると
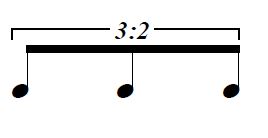
音価Lは=166.666666…(ms)です。
このとき8分音符の音価は250(ms)、16分音符の音価は125(ms)なので
250(ms) ≧ 166.666666… (ms) > 125 (ms)
となり
8分音符の音価(ms) ≧ 1拍3連の音価(ms) > 16分音符の音価(ms)
が成り立つので、「符尾・連桁の数」は1つになるわけです。
「対数」と「x分音符の値」を使って、符尾・連桁の数を計算する
さて。
仕組みが分かったところで、いちいち音符の長さを求めて比較するのは面倒です。
それに、アルゴリズムとして美しくありません。
「x分音符」の値を使って、以下の対数を使った計算をすれば「符尾・連桁の数」が一発で分かります。
log2(x) – 2 (の整数部分を見る)
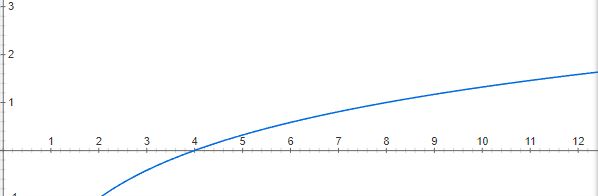
縦軸yは 「符尾・連桁の数」で、横軸xは「x分音符のx値」になります。
実際に計算してみる
たとえば、さきほどのBPM=120「1拍3連」の 「符尾・連桁の数」 は…
まず、BPM=120の全音符は2000(ms)のため
2000(ms)÷166.666666…(ms)≒12
で
「1拍3連」↑は、分音符だけで表すと「12分音符」であると分かります。
では、上の計算式に当てはめて
log2(12) – 2 = 1.5849625….
整数部分は1です。
したがって、「1拍3連」は「符尾・連桁の数」が1つの音符だと分かります。
同じく「16分音符」や「1拍5連」は、の整数部分の値が2になるので「符尾・連桁の数」が2であると分かります。
ちなみに、この値が0以下の時は、 「符尾・連桁の数」 は0になります。
「-2」の時は全音符、「-1」の時は2分音符、「0」の時は4分音符を表しています。
この辺りはプログラムを書く場合は、「if文」を使って処理しています。
面倒な計算は機械にやらせよう
さて。
ここまで読んで「こんなのいちいち計算するの面倒くさいだろ…!」と思ったと思います。笑
その通りです!!笑
僕もいちいち考えているのではなく、プログラムを組んで使っています。
実際にここまで紹介した内容を元に作ったウェブアプリがこちらです。↓
https://o-to.khufrudamonotes.com/o-to-metric-modulation
ぜひ、使ってみてください!(๑˃̵ᴗ˂̵)و
「メトリックモジュレーション」を考える
ここまでのことを踏まえて、メトリックモジュレーションを考えます。
…しかし、長くなったので別記事にまとめました。笑
「ポリリズム」を考える
最後は、「ポリリズム」について考えて終わりにしたいと思います。
しかし、こちらも長くなり過ぎたので別記事にまとめました。笑
音楽を論理的に考えること
音楽は「芸術」であり、なんとなく不思議で、捉えどころがないと思われがちです。
たしかに、「なぜ人間はメジャーコードを明るく、マイナーコードを暗く感じるか…」など、不思議な部分も多くあります。
しかし、反対に「音」は物理現象です。
物理現象を扱っているので、論理的に理解できる部分も多くあるわけです。
個人的には、「多くの人が「芸術」というブラックボックスに入れてしまった要素を少しでも論理的に考えることには、意義があるのではないかな…」と思います。
おわりに:リズムに興味を持ったきっかけ
ここまで読んだ方、お疲れ様でした。笑
最初にも書いたように、僕がリズム対して色々と考え始めたのは、今から10年以上前です。
当時、L’Arc-en-Cielのドラムコピーをするために、アクセントが2拍4拍ではない、いわゆるスリップビートの練習をしていました。
…すると、ある時
「アクセントをずらしていくと、全然4拍子に聴こえなくなる時があるなぁ… ていうか、なんかこれ3拍子やシャッフルっぽくない!?」
とメトリックモジュレーションの仕組みに気付きました。
あの瞬間は、かなりテンションが上がってEurekaみを感じました。笑
( 「メトリックモジュレーション」という概念自体は後で知りました。)
それから約10年、色々とリズムについて考えてきました。
そして、ついに今回自分の考えを一通りまとめられたので、わりと感慨無量です。
もちろん、まだまだ追及が足りない部分もあるかもしれません。
しかし、この記事を読んだ人が少しでもリズムに対して考えるきっかけになればうれしいです。
では!(๑˃̵ᴗ˂̵)و
参考文献・URL
菊地成孔 ”ビュロー菊地チャンネル「モダンポリリズム講義 第一回」”
教育出版 音楽の小部屋 音楽四方山話 楽譜編
https://www.kyoiku-shuppan.co.jp/docs/music/kobeya/hondana/mamechishiki_1_2.html
『音楽と数学の交差』桜井 進/坂口 博樹